Даже при создании фантастического фильма не зазорно принять во внимание ограничения, накладываемые законами природы на межзвездные путешествия. Прогресс в технологии позволит со временем приблизиться к этим пределам, но нельзя их превзойти.
Лет шесть назад мне довелось переводить статью
Bernard M. Oliver. A Review of Interstellar Rocketry Fundamentals // Journal of The British Interplanetary Society Vol.43. pp.259-264, 1990.
Порывшись в архиве, я нашел ее, проверил выкладки и сделал расчеты применительно к описанному в ТА путешествию.
Тантра – классическая ракета. Запас топлива и энергии хранится на борту. Скорость полета равна `\frac{5}{6}c`. Только при таком громадном значении скорости возможно достижение описанных в ТА объектов за разумное время. Иначе ткань повествования порвется сразу во многих местах.
В романе подразумевается шесть циклов разгона (торможения): от Земли к Зирде, у Зирды, к месту рандеву с Альграбом, к Земле и окончательное торможение. Два цикла разгона представляются мне излишними. Лучше уж сразу лететь к Земле, чем тратить уйму топлива на полет к системе Б-7336-С+87-А. Вдобавок, наматывая там круги инферно, Тантра для поддержания обращения должна прирастить свою скорость еще как минимум на половину `c`. Гораздо рациональней ожидать Альграб где-нибудь на окраине системы Зирды.
Этот эпизод в романе всегда казался мне непродуманным. Если планета К-2-2Н-88 хорошо известна как удобное место рандеву звездолетов и если встреча там была запланирована, то расчет пути оттуда к Земле должен быть тоже заранее подготовлен. Если же принять, что Тантра ждет Альграб в системе Зирды, то, тем более, возвращаться следовало по своему следу. Непонятно, почему обратный курс проложен через некую неисследованную область.
Итак, наиболее подробно остановлюсь на варианте четырех циклов разгона-торможения. Предполагается, что кпд двигателя 100%, т.е. отсутствуют тепловые и иные потери; вся энергия топлива преобразуется в упорядоченную кинетическую энергию продуктов истечения.
Массовое число `\mu` – отношение массы ракеты перед стартом к массе после финиша. Следовательно, отношение массы топлива к массе полезной нагрузки `m` равно `\mu-1`.
Кинетическая энергия ракеты `T`.
Кинетическая энергия топлива `E`. Не превосходит `T`.
Кинематическая эффективность `\eta=\frac{E}{T}`. Кинематическая эффективность ракеты была бы равна единице (100%), если бы все продукты истечения покоились относительно пункта назначения. Для этого скорость продуктов истечения должна изменяться таким образом, чтобы в каждый момент оставаться равной скорости полета ракеты. Но такая идеально экономичная ракета нереализуема, поскольку самостоятельно стартовать не может.
За один разгон (без торможения): `T_1=`0,809
Два разгона (путешествие в один конец): `T_2=`4,545
Четыре разгона (путешествие туда и обратно): `T_4=`59,5
Шесть разгонов: `T_6=`664,5
Здесь и далее единицей измерения энергетических величин является энергия покоя полезной нагрузки `mc^2`.
Остальные искомые параметры зависят от скорости истечения. Рассмотрим несколько вариантов.
Если скорость истечения в точности равна скорости света, то продуктом истечения являются фотоны (фотонная ракета). Массовое число получается минимальным среди всех возможных вариантов.
Один разгон:
`\mu_1`=3,317, `E_1=`2,317, `\eta_1=`0,349
Два разгона:
`\mu_2=`11, `E_2=`10, `\eta_2=`0,455
Четыре разгона:
`\mu_4=`121, `E_4=`120, `\eta_4=`0,496
Шесть разгонов:
`\mu_6=`1331, `E_6=`1330, `\eta_6=`0,5
Однако минимум топлива не означает минимум энергии. Фотонная ракета имеет низкую кинематическую эффективность. Она может быть повышена только путем уменьшения скорости истечения, т.е. ценой увеличения массового числа.
Пусть скорость истечения ракеты постоянна, но не обязательно равна `c`. Тогда существует оптимальное ее значение (для четырех разгонов равное 0,968`c`), при котором кинематическая эффективность максимальна:
`\eta_4=`0,564, `\mu_4=`142, `E_4=`105,5.
Энергия, содержащаяся в единичной массе топлива, должна быть в 1,335 раз меньше ее энергии покоя. Таким образом, экономия энергии получается совсем небольшая, но важно, что продуктами истечения могут быть частицы с ненулевой массой.
Доказано, что оптимальной в плане повышения `\eta` является ракета с постоянной скоростью продуктов истечения относительно пункта назначения. Чем меньше данная скорость, тем выше `\eta`, но больше и `\mu`.
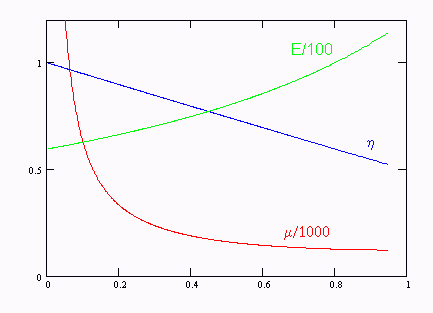
В свою очередь, данная скорость связана с удельной энергоемкостью топлива, если считать, что вся энергия сосредоточена в топливе. На графике энергоемкость топлива отложена вдоль оси абсцисс в долях энергии аннигиляции. Единичное значение соответствует фотонной ракете.

Видно, как быстро возрастает `\mu` с уменьшением энергоемкости.
Можно решить задачу о нахождении оптимальной энергоемкости, при которой как `\mu`, так и `E` имеют одинаковое относительное отклонение от своих минимальных значений. Последнее получается равным 33,7% при энергоемкости топлива 0,495. Это для четырех разгонов. Для двух соответственно 37,5% и 0,442. Итак, оптимальная (в указанном смысле) удельная энергоемкость чуть менее половины аннигиляционной.
01 июня 2006, 22:35